dataninja

Goal

Algorithms for decision support, optimization and machine learning contain parameters that influence their behavior and the way they solve problems. Adjusting these parameters can lead to faster performance and/or higher quality solutions. However, finding good parameters is a difficult task, especially when the data received as input changes over time. Our project harnesses the learning power of multi-armed bandit (MAB) methods to adjust the parameters of algorithms in realtime over the course of problem solving.

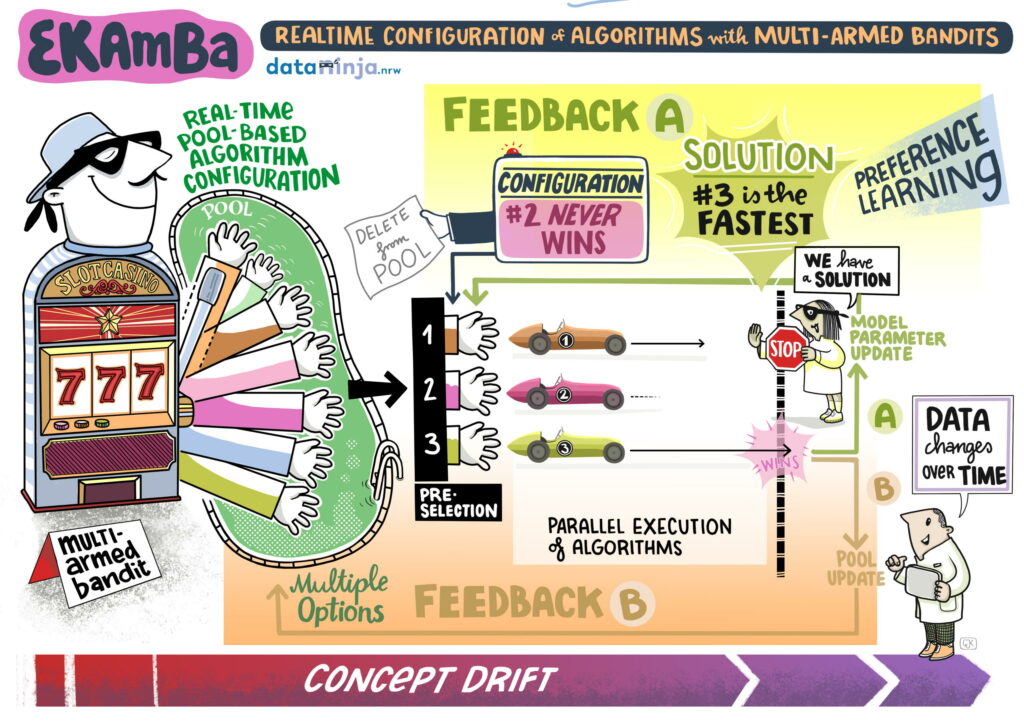
Project Overview

The parameters of an algorithm have an influence on its problem-solving behavior and hence its performance on specific problem instances. For example, depending on how skillful its parameters are set, an algorithm for solving traveling salesperson (TSP) problems may run faster or slower on a concrete TSP instance or may produce better or worse solutions (an approximation to the optimum). Algorithm configuration (AC) refers to the task of automatically adjusting the parameters of an algorithm on a per-instance basis, i.e., tailoring the parameters to a specific problem instance^​1​. We are especially interested in a practically motivated pool-based scenario, where problems of the same type are solved repeatedly, and several algorithms are run on each problem instance in parallel. In this context, parameters ought to be adjusted in real-time.

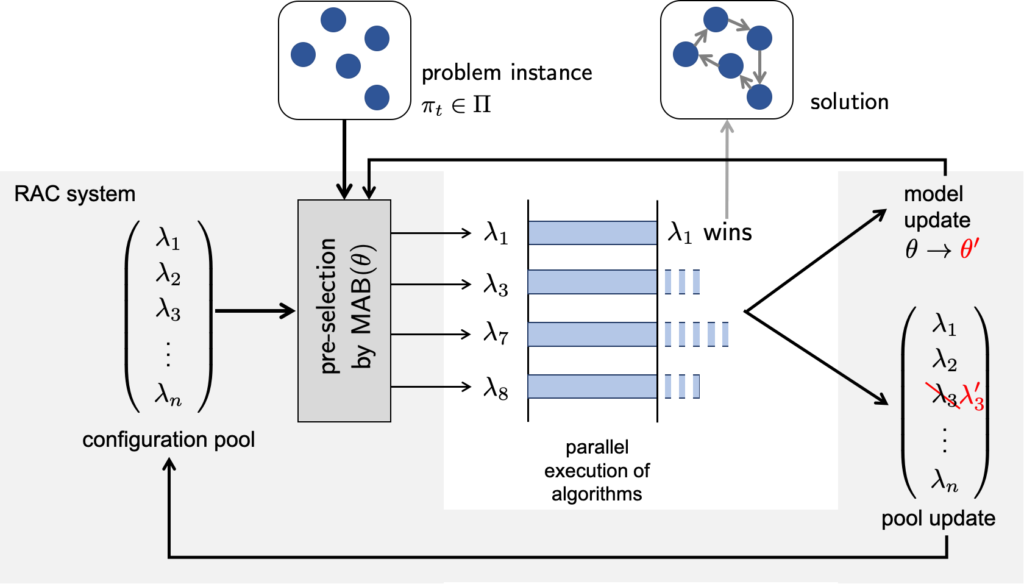
To tackle the AC problem, we make use of multi-armed bandit algorithms, a class of machine learning methods for sequential decision making under uncertainty^​2​. More concretely, we will develop new types of MAB algorithms specifically tailored to our setting, which are able to choose high-quality parameters even as the underlying distribution of problems drifts over time. To this end, we will mainly build on so-called preselection bandits^​3​, a recent class of bandit algorithms that is well suitable to formalize the pool-based variant of real-time AC^​4​.

Preliminary Results

As a first step, we wrote a literature review on the current state of algorithm configuration. The review provides an up-to-date overview of AC methods presented in the literature and their applicability for different problem settings. In particular, we provide the first taxonomy that structures methods and problem settings according to their characteristics. In addition, we look at the current state of industry adoption and provide a glimpse into the future of AC by aggregating and discussing unsolved problems and further work directions.

Furthermore, we have developed an algorithmic framework to find an optimal arm in a combinatorial bandit scenario, a generalization of the classical multi-armed bandit problem, in which in each time step an entire set of arms can be “pulled” simultaneously. The algorithm is quite general in its design such that it can be instantiated for a combinatorial bandit scenario, where either numerical reward values are received for each arm contained in the “pulled” set of arms, or feedback is obtained in the form of a qualitative comparison between the arms (preference feedback). From a practical point of view, this algorithm can also be applied in the context of algorithm configuration by interpreting the available configurations as arms that can be executed (i.e. “pulled”) in parallel on our computational resources. Our experiments show that stopping the parallel solution process once a configuration is finished and providing the corresponding preference feedback to the algorithm (i.e., which configuration finished first?) leads to good empirical results in finding suitable configurations.

Project Publications

• Brandt, Jasmin, Viktor Bengs, Björn Haddenhorst, and Eyke Hüllermeier (2022). ‘‘Finding Optimal Arms in Non-stochastic Combinatorial Bandits with Semi-bandit Feedback and Finite Budget’’. In: Advances in Neural Information Processing Systems (NeurIPS). url: https://openreview.net/forum?id=h37KyWDDC6B.
• Brandt, Jasmin, Björn Haddenhorst, Viktor Bengs, and Eyke Hüllermeier (2024). ‘‘Dueling Bandits with Delayed Feedback’’. In: Proceedings of the DataNinja sAIOnARA Conference, pp. 29–31. doi: 10.11576/dataninja-1163.
• Brandt, Jasmin, Elias Schede, Viktor Bengs, Björn Haddenhorst, and Eyke Hüllermeier (2022). ‘‘Finding Optimal Arms in Non-stochastic Combinatorial Bandits with Applications in Algorithm Configuration’’. In:Proceedings of the Sixth Conference on From Multiple Criteria Decision Aid to Preference Learning (DA2PL).
• Brandt, Jasmin, Elias Schede, Björn Haddenhorst, Viktor Bengs, Eyke Hüllermeier, and Kevin Tierney (2023). ‘‘AC-Band: A Combinatorial Bandit-Based Approach to Algorithm Configuration’’. In: Thirty-Seventh AAAI Conference on Artificial Intelligence, 2023. AAAI Press, pp. 12355–12363. doi: 10.1609/AAAI.V37I10.26456. url: https://doi.org/10.1609/aaai.v37i10.26456.
• Brandt, Jasmin, Elias Schede, Shivam Sharma, Viktor Bengs, Eyke Hüllermeier, and Kevin Tierney (2023). ‘‘Contextual Preselection Methods in Pool-based Realtime Algorithm Configuration’’. In: Proceedings of the LWDA 2023 Workshops, Marburg (Germany), Oktober 9-11th, 2023. CEUR Workshop Proceedings. CEUR-WS.org, pp. 492–505.
• Brandt, Jasmin, Elias Schede, Kevin Tierney, and Eyke Hüllermeier (2021). ‘‘EKAmBa: Realtime Configuration of Algorithms with Multi-armed Bandits’’. In: Workshop on “Trustworthy AI in the Wild” at 44th German Conference on Artificial Intelligence (KI).
• Brandt, Jasmin, Marcel Wever, Viktor Bengs, and Eyke Hüllermeier (2024). ‘‘Best Arm Identification with Retroactively Increased Sampling Budget for More Resource-Efficient HPO’’. In: Proceedings of the Thirty-Third International Joint Conference on Artificial Intelligence, (IJCAI). International Joint Conferences on Artificial Intelligence Organization, pp. 3742–3750.
• Haddenhorst, Björn, Viktor Bengs, Jasmin Brandt, and Eyke Hüllermeier (2021). ‘‘Testification of Condorcet Winners in Dueling Bandits’’. In:Proceedings of the Thirty-Seventh Conference on Uncertainty in Artificial Intelligence (UAI). Vol. 161. Proceedings of Machine Learning Research, pp. 1195–1205.
• Schede, Elias, Jasmin Brandt, Alexander Tornede, Marcel Wever, Viktor Bengs, Eyke Hüllermeier, and Kevin Tierney (2022). ‘‘A Survey of Methods for Automated Algorithm Configuration’’. In: J. Artif. Intell. Res. 75, pp. 425–487. doi: 10.1613/jair.1.13676. url: https://doi.org/10.1613/jair.1.13676.

Cooperation

Decision and Operation Technologies Group

Prof. Dr. Kevin Tierney

PhD student: Elias Schede

Data Science Group

Prof. Dr. Axel-Cyrille Ngonga Ngomo

PhD student: Jasmin Brandt

References