dataninja

Interpretable machine learning through game-theoretical analysis of influencing variables and interaction effects

Goal

Most machine learning (ML) methods assume a representation of data entities in terms of a fixed set of variables (features). Analyzing the importance of individual variables for a model induced from the data, or for the prediction made with that model in a specific situation, facilitates the interpretation of ML models and supports subtasks such as feature selection. The goal of this project is to develop novel methods for feature analysis. In particular, we are interested in numerical measures quantifying the importance of individual variables in a machine learning task, i.e., the contribution of individual variables to the task at hand and predictions made by a model, as well as the interaction and dependencies between different variables.

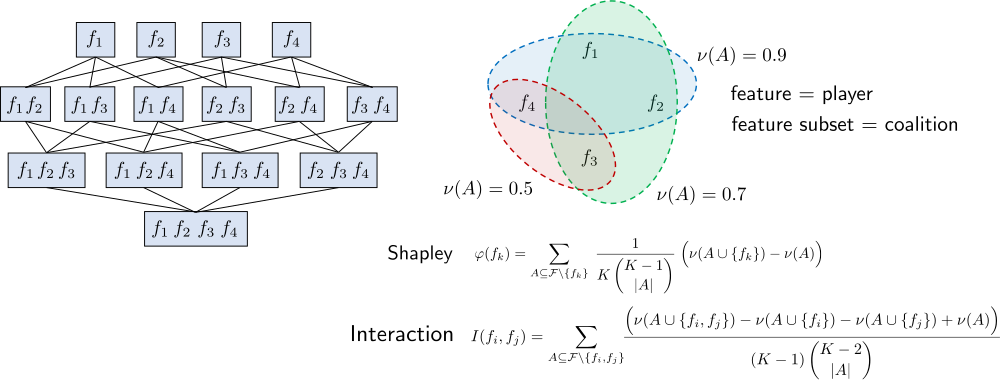
Project Overview

This project aims at transparent modeling of dependencies and interactions between variables as well as theoretically justified reductions of nonlinear dependencies to understandable and interpretable measures for the influence of individual variables, both for supervised and unsupervised learning. A theoretical framework of that kind shall be complemented by suitable visualization techniques to further facilitate interpretation, the interaction with users and domain experts, and the exploration of dependencies in high-dimensional data spaces. All methods shall be evaluated in various case studies in the medical domain.

The main innovation of the project is to establish a connection between feature analysis and (cooperative) game theory. To this end, a feature subset is considered as a coalition in game theory, and the performance of a model trained with these features as the value of the coalition. The importance of individual variables can then be quantified in terms of well-established game-theoretical measures, such as the Shapley value, just like the interaction between pairs or groups of variables. Due to the exponential size of the lattice of feature subsets, the exact computation of such quantities is in general infeasible. Therefore, a key challenge of the project is the development of efficient approximate algorithms.

^​1–4​

Current Work

Identifying Top-k Players in Cooperative Games via Shapley Bandits
The formal notion of a cooperative game, in which players can form coalitions to accomplish a
certain task, is a versatile concept with countless practical applications. In the context of (supervised) machine learning, individual features can be seen as players and feature subsets as coalitions – the task here is to train a model with high predictive performance^​2,5​. An interesting question in the context of cooperative games concerns the importance or contribution of an individual player: How to distribute the collective benefit of a coalition among the individual players? Independent of the considered application, cooperative game theory has proposed different solution concepts, with the Shapley value as the arguably most popular one^​6​.

Due to the computational effort growing exponentially with the number of participants in a game, several methods have been proposed to approximate Shapley values. Yet, in many applications, only the order of players according to their Shapley values is important, or maybe the set of the 𝑘 best players, but not the values themselves. We consider the problem of identifying the 𝑘 players in a cooperative game with the highest Shapley values and denote it as the Top-k Shapley problem. By viewing the marginal contributions of a player as a random variable, we establish a connection between cooperative games and multi-armed bandits, which in turn allows us to reduce Top-k Shapley to the multiple arms identification problem. We call the resulting bandits problem Shapley bandits. Besides adopting existing algorithms for multiple arms identifications, we propose the Border Uncertainty Sampling algorithm (BUS) and provide empirical evidence for its superiority over state-of-the-art algorithms.

Non-Stationary Dueling Bandits
The dueling bandits problem is an online decision making problem in which a learner has to repeatedly select a pair of items, upon he observes a noisy binary preference feedback of stochastic nature. The learner’s goal is to play as often as possible over a given time horizon pairs that contain the best item, where we define the best item to be the Condorcet Winner, i.e., the item that beats all others with probability greater than half. The innovation of our setting is the introduction of non-stationarity. In particular, the underlying hidden preferences are not fixed in time, but are likely to change. We motivate this by the observation that user preferences tend to shift over time in various contexts. We propose with Beat the Winner Reset (BtWR) an algorithm for which we not only prove satisfying results for the novel non-stationary setting, but also discover its asymptotic superiority over current state-of-the-art algorithms (for example, see ^​7,8​). We are optimistic that the combination of our previously established connection between Shapley values and multi-armed bandits and the work on non-stationary dueling bandits opens up new room for research questions and methodology to be discovered.

Project Publications

• Balestra, Chiara (2024). ‘‘Is it Possible to Characterize Group Fairness in Rankings in Terms of Individual Fairness and Diversity?’’ In: DataNinja sAIOnARA Conference, pp. 10–12. doi: 10.11576/dataninja-1157.
• Balestra, Chiara, Antonio Ferrara, and Emmanuel Müller (2024). ‘‘FairMC Fair–Markov Chain Rank Aggregation Methods’’. In: International Conference on Big Data Analytics and Knowledge Discovery. Springer, pp. 315–321.
• Balestra, Chiara, Florian Huber, Andreas Mayr, and Emmanuel Müller (2022). ‘‘Unsupervised Features Ranking via Coalitional Game Theory for Categorical Data’’. In: Big Data Analytics and Knowledge Discovery – 24th International Conference, DaWaK 2022, Vienna, Austria, August 22-24, 2022, Proceedings. Ed. by Robert Wrembel, Johann Gamper, Gabriele Kotsis, A Min Tjoa, and Ismail Khalil. Vol. 13428. Lecture Notes in Computer Science. Springer, pp. 97–111. doi: 10.1007/978-3-031-12670-3\_9. url: https://doi.org/10.1007/978-3-031-12670-3%5C_9.
• Balestra, Chiara, Bin Li, and Emmanuel Müller (2023a). ‘‘On the Consistency and Robustness of Saliency Explanations for Time Series Classification’’. In: KDD 2023, 9th International Workshop on Mining and Learning from Time Series (MILETS).
• Balestra, Chiara, Bin Li, and Emmanuel Müller (2023b). ‘‘slidSHAPs–sliding Shapley Values for correlation-based change detection in time series’’. In: 2023 IEEE 10th International Conference on Data Science and Advanced Analytics (DSAA). IEEE, pp. 1–10.
• Balestra, Chiara, Carlo Maj, Emmanuel Müller, and Andreas Mayr (2023a). ‘‘Redundancy-aware unsupervised ranking based on game theory: Ranking pathways in collections of gene sets’’. In: Plos one 18.3, e0282699.
• Balestra, Chiara, Carlo Maj, Emmanuel Müller, and Andreas Mayr (2023b). ‘‘Redundancy-aware unsupervised rankings for collections of gene sets’’. In: KDD 2023, 22nd International Workshop on Data Mining in Bioinformatics (BIOKDD).
• Balestra, Chiara, Andreas Mayr, and Emmanuel Müller (2024). ‘‘Ranking evaluation metrics from a group-theoretic perspective’’. In: arXiv preprint arXiv:2408.16009.
• Fumagalli, Fabian, Maximilian Muschalik, Patrick Kolpaczki, Eyke Hüllermeier, and Barbara Hammer (2023). ‘‘SHAP-IQ: Unified Approximation of any-order Shapley Interactions’’. In: Proceedings of Advances in Neural Information Processing Systems (NeurIPS).
• Fumagalli, Fabian, Maximilian Muschalik, Patrick Kolpaczki, Eyke Hüllermeier, and Barbara Hammer (2024). ‘‘KernelSHAP-IQ: Weighted Least Square Optimization for Shapley Interactions’’. In: Proceedings in International Conference on Machine Learning, (ICML).
• Klüttermann, Simon, Chiara Balestra, and Emmanuel Müller (2024). ‘‘On the Efficient Explanation of Outlier Detection Ensembles Through Shapley Values’’. In: Pacific-Asia Conference on Knowledge Discovery and Data Mining. Springer, pp. 43–55.
• Kolpaczki, Patrick (2024). ‘‘Comparing Shapley Value Approximation Methods for Unsupervised Feature Importance’’. In: Proceedings of DataNinja sAIOnARA 2024 Conference, pp. 13–15. doi: 10.11576/DATANINJA-1158.
• Kolpaczki, Patrick, Viktor Bengs, and Eyke Hüllermeier (2021). ‘‘Identifying Top-k Players in Cooperative Games via Shapley Bandits’’. In: Proceedings of the LWDA 2021 Workshops: FGWM, KDML, FGWI-BIA, and FGIR, pp. 133–144.
• Kolpaczki, Patrick, Viktor Bengs, Maximilian Muschalik, and Eyke Hüllermeier (2024). ‘‘Approximating the Shapley Value without Marginal Contributions’’. In: Proceedings of AAAI Conference on Artificial Intelligence (AAAI), pp. 13246–13255.
• Kolpaczki, Patrick, Georg Haselbeck, and Eyke Hüllermeier (2024). ‘‘How Much Can Stratification Improve the Approximation of Shapley Values?’’ In: Proceedings of the Second World Conference on eXplainable Artificial Intelligence (xAI), pp. 489–512.
• Kolpaczki, Patrick, Eyke Hüllermeier, and Viktor Bengs (2024). ‘‘Piecewise-Stationary Dueling Bandits’’. In: Transactions on Machine Learning Research. issn: 2835-8856.
• Kolpaczki, Patrick, Maximilian Muschalik, Fabian Fumagalli, Barbara Hammer, and Eyke Hüllermeier (2024). ‘‘SVARM-IQ: Efficient Approximation of Any-order Shapley Interactions through Stratification’’. In: Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), pp. 3520–3528.
• Li, Bin, Chiara Balestra, and Emmanuel Müller (2022). ‘‘Enabling the Visualization of Distributional Shift using Shapley Values’’. In: NeurIPS 2022 Workshop on Distribution Shifts: Connecting Methods and Applications. url: https://openreview.net/forum?id=HxnGNo2ADT.
• Muschalik, Maximilian, Hubert Baniecki, Fabian Fumagalli, Patrick Kolpaczki, Barbara Hammer, and Eyke Hüllermeier (2024). ‘‘shapiq: Shapley Interactions for Machine Learning’’. In: Proceedings Advances in Neural Information Processing Systems (NeurIPS) Datasets and Benchmarks Track.

Cooperation

Data Science and Data Engineering

Prof. Dr. Emmanuel Müller

PhD student: Chiara Balestra

Communications Engineering Group

Prof. Dr. Rainhold Häb-Umbach

PhD student: Patrick Kolpaczki

References