dataninja

Goal

The GAIA project aims to explore Gaussian processes for efficient detection and interpretation of anomalies in multivariate time series data. In particular, we aim to investigate unsupervised Gaussian processes in order to identify, understand and resolve underlying correlations and anomalies. In order to learn Gaussian process models in a scalable and real-time manner, we intend to develop new streaming algorithms, which will be implemented in an open source manner and with reference to industrial standards, and tested in application-oriented scenarios, together with industry partners.

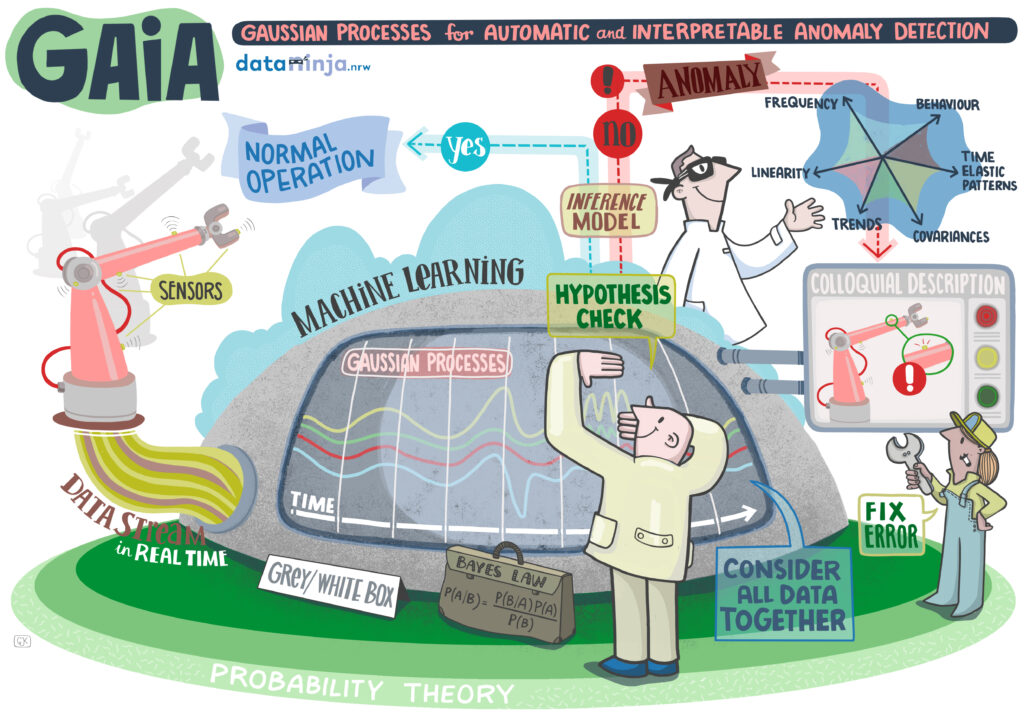
Project Overview

Gaussian Process Models are widely used in Bayesian Machine Learning as they can be applied when only limited data is available and can be directly interpreted. The GAIA project will employ such Gaussian Process Models in an extension to multivariate time series. The resultant model will therefore cover spatial as well as temporal information and should detect anomalies spanning both of these dimensions. On focus will be on how model selection influences the explainability of constructed models.

A latent variable model can be used, for example, to represent a process as is found in many industrial applications. Such processes are characterized through temporal data given as time series. In the project, a latent variable model should be learned in an unsupervised fashion as a Gaussian Process Model. Importantly, prior knowledge on the particular application domain can be exploited: While usually in Gaussian Processes the search for a fitting covariance function is expensive, domain knowledge can be introduced into the covariance matrix in the form of underlying differential equations which leads to hybrid and interpretable models.

During the first year, we managed to produce first results and a first implementation for physical data driven hybrid Gaussian Processes. Further, we supervised a successful Bachelor’s thesis on model selection, whose results we will further investigate.
Finally, we developed a novel model search algorithm for Gaussian processes on data streams and published a first evaluation.

^​1–4​

Project Publications

• Besginow, A., Hüwel, J. D., Lange-Hegermann, M., & Beecks, C. (2020). Exploring Methods to Apply Gaussian Processes in Industrial Anomaly Detection. Neurocomputing, 403, 383-399.
• Hüwel, J. D., Berns, F., & Beecks, C. (2021, December). Automated Kernel Search for Gaussian Processes on Data Streams. In 2021 IEEE International Conference on Big Data (Big Data) (pp. 3584-3588). IEEE.
• Berns, F., Hüwel, J. D., & Beecks, C. (2021, December). LOGIC: Probabilistic Machine Learning for Time Series Classification. In 2021 IEEE International Conference on Data Mining (ICDM) (pp. 1000-1005). IEEE.
• Berns, F., Hüwel, J. & Beecks, C. Automated Model Inference for Gaussian Processes: An Overview of State-of-the-Art Methods and Algorithms. SN COMPUT. SCI. 3, 300 (2022).

Cooperation

Data Management and Analytics Group

Prof. Dr. Christian Beecks

PhD student: Jan-David Hüwel

Department of Electrical Engineering and Computer Science

Prof. Dr. Markus Lange-Hegermann

PhD student: Andreas Besginow

References