Explaining Machine Learning through Feature Importance Scores and Interaction Effects based on Game Theory

In the hunt for better predictive performances, machine learning models have become increasingly more complex and opaque. While this development is favorable at first, it also comes with the growing burden of understanding their decision-making. The rising demand in answers for questions such as “Why did the model predict a certain outcome?” or “What information had the most influence on the model?” posed by human end users, developers, or even legislative regulators poses a challenge.

What are additive feature explanations?

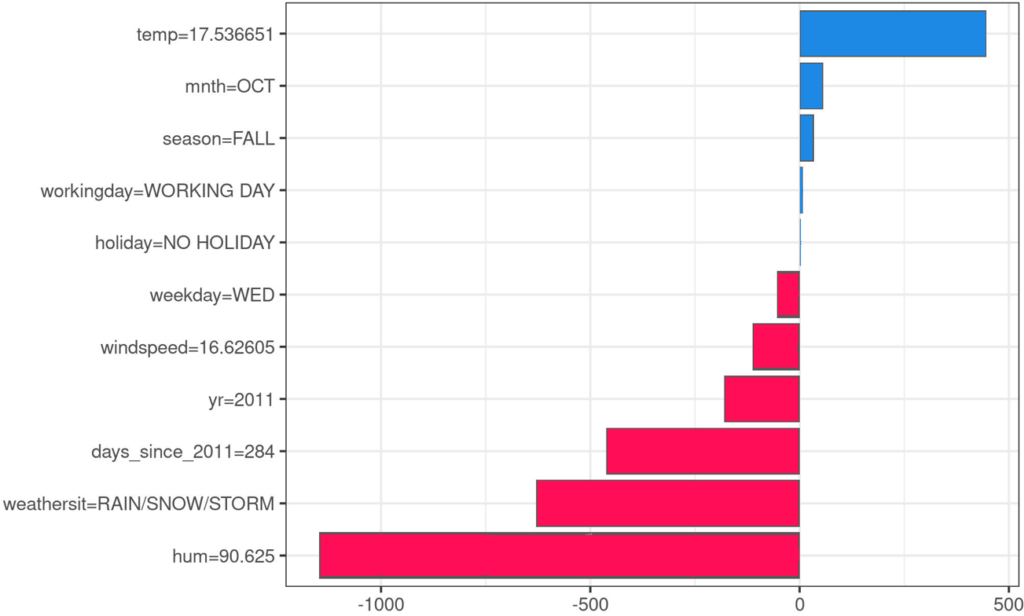
We would like to interpret the feature importance scores such that each score indicates who much a feature contributed to an effect of our interest. This could be the the model’s predicted value for a particular instance (a single patient) or the predictive performance over a set of instances (database of patients) when all features are used. It would allow us to conclude that, although simplifying, adding the information that a feature contains, increases the considered effect by the amount of its score. Hence, the total value achieved by using all features together is split among them such that the sum of individual scores adds up back to that value. This additive type of explanation is simple and easy to comprehend for humans. Besides looking at a predicted value (local feature attribution) or predictive performance (global feature importance), additive explanations can also be used to evaluate the importance of datapoints or neurons in networks.

How to divide a reward fairly? The origin of the Shapley value

The central question of additive explanations is how exactly to split that observed value among the features. Splitting it evenly wouldn’t do justice to the highly important features and also provide no useful explanation. There must be a way to account for the fact that some features contribute more than others. This task can be modeled as a cooperative game stemming from game theory.
Abstractly speaking, player or agents (that represent features) can form groups, so called coalitions, in which they cooperate and achieve a collective reward that is to be divided among them. In our case, the features cooperate by the model’s usage of their provided information. And the achieved predictive performance, such as 90% classification accuracy, can be taken as the reward (value of the coalition). Dividing this reward among the players yields our desired importance scores.

People commonly demand specific properties from a division that are intuitive and capture a sense of fairness. Obviously, a player whose inclusion does not increase the reward for any coalition, should also obtain a score of zero. Or for example, if two players interchangeable, meaning that swapping them does not change the value of any coalition, then both should be assigned equal scores.

Interestingly, it turns out that there is only one way to split the rewards while fulfilling all of these properties simultaneously! It is the Shapley value. The Shapley value assigns each player a fair share of the total reward based on what all coalitions achieve. In other words: if one demands these fairness properties then the Shapley value has to be used as it is the only solution, which is why it has enjoyed huge popularity in recent years, in and outside of explainability.

Interaction effects: When single importance values are not enough

Additive feature explanations that provide individual importance scores may have attracted extensive attention but are certainly not flawless or at least not all-revealing. In fact, there exists even criticism how they could potentially mislead inexperienced users. More important to us, the additivity is too simple and does not capture an important interplay that happens between the features.

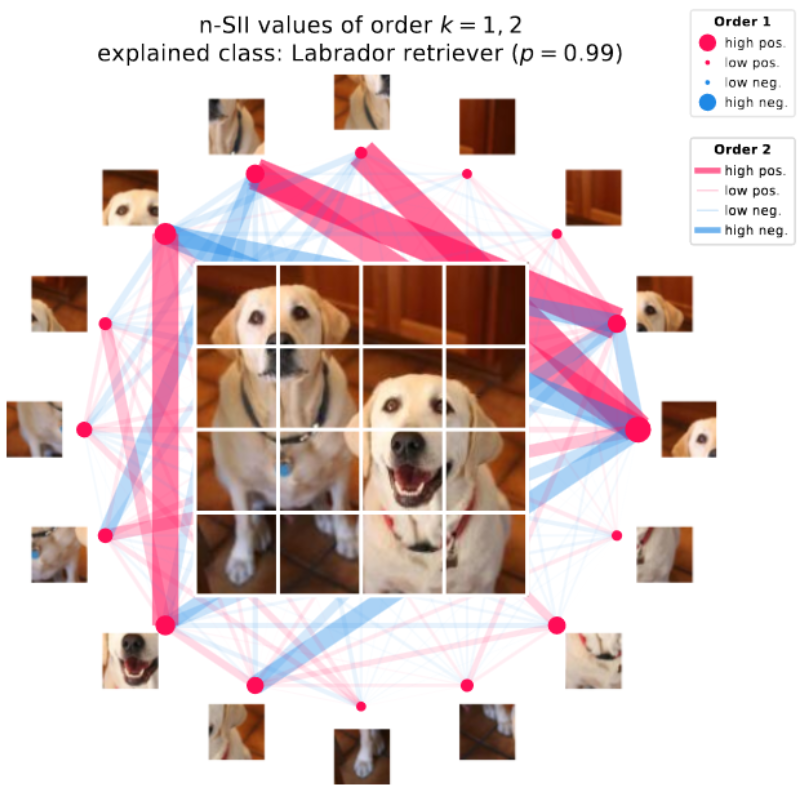
Features affect each other and have synergies between them, which we call interaction. The sheer presence of one feature can impact the contribution of another feature. Coming back to our initial example, the information of a certain genetic marker (that indicates the blood type) renders the blood type feature redundant (negative interaction). Or the other way round, it could well happen that only the combination of two features reveals something insightful while these on their own in isolation provide no information (positive interaction).

Fortunately, game theory extends the Shapley value to Shapley interaction providing a notion of interaction between players in cooperative games, which is also based on desirable properties. We seek not to replace importance scores but to extend them by quantifying interactions and thus enrich additive feature explanations.

The approximation problem of the Shapley value and Shapley interactions

Unfortunately, despite its nice properties the Shapley value, and the notion of interaction as well, does not come without a drawback. In order to calculate it, all possible coalitions of players need to be evaluated and their exponential number renders this task practically infeasible for even medium-sized feature numbers.

Take for example a dataset consisting of just 20 features. One would need to retrieve the value of more than a million coalitions. This might discourage to use the Shapley value but there exists an elegant remedy to this problem. Instead of computing the features’ Shapley values exactly, we can approximate them, trying to obtain precise estimates as quickly as possible. This challenge has already claimed its own research branch and studies approximation algorithms and theoretical guarantees for the precision of the returned estimates.

Our contribution: versatile approximation methods for fast and reliable Shapley estimates

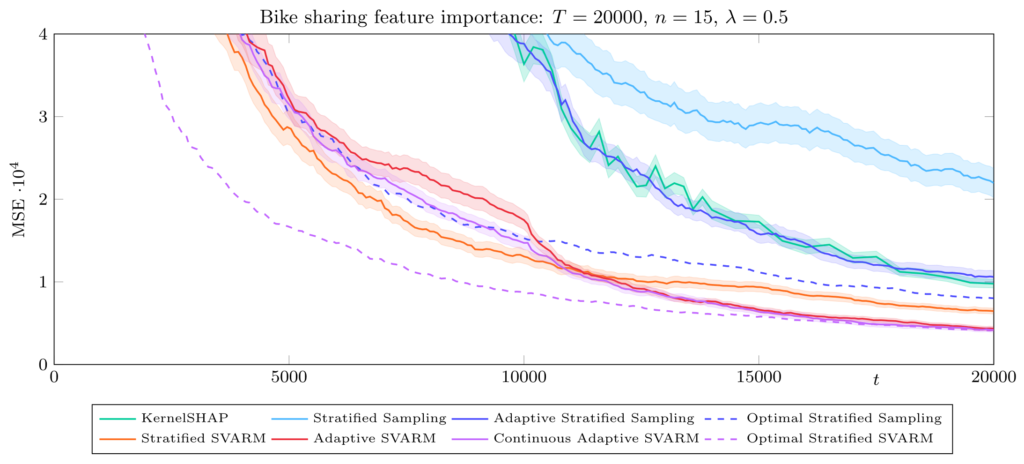
We contributed to explainability and trustworthy AI by providing novel approaches for approximating the Shapley value and Shapley interactions. Within the approximation problem we distinguish between two different tasks: First, that of estimating all features’ Shapley values precisely, measuring precision by how much these estimates deviate from their respective true values. And second, the identification of the top-k players with he highest Shapley values.

The subtle difference lies within the opportunity that not all players’ estimates need to be (equally) precise and just knowing which of them have a higher value than that in k-th position already suffices. Depending on the effect of interest our approximation algorithms for the Shapley value reach state-of-the-art empirical performances, and those for interactions have set the new benchmark to beat.

In addition, our theoretical analyses allow to state guarantees on their approximation error, providing further understanding of when to use them best and insight to this research field. Worth mentioning is our credo, to develop methods that are model-agnostic and even domain-independent. These methods are applicable to any machine learning model and data. Further, they can also be employed outside of the realm of machine learning, such as operations research, finance, and social sciences as long as a cooperative game consisting of players and a reward mechanism can be formulated.

Additional resources

To make Shapley interactions accessible to a broader community we developed the code package shap-iq: https://github.com/mmschlk/shapiq
This package allows to retrieve interactions for various tasks on your own model and data.
In addition, several approximation algorithms including your own can be benchmarked to accelerate this research field.

Cooperation

Project Publications

• Balestra, Chiara (2024). ‘‘Is it Possible to Characterize Group Fairness in Rankings in Terms of Individual Fairness and Diversity?’’ In: DataNinja sAIOnARA Conference, pp. 10–12. doi: 10.11576/dataninja-1157.
• Balestra, Chiara, Antonio Ferrara, and Emmanuel Müller (2024). ‘‘FairMC Fair–Markov Chain Rank Aggregation Methods’’. In: International Conference on Big Data Analytics and Knowledge Discovery. Springer, pp. 315–321.
• Balestra, Chiara, Florian Huber, Andreas Mayr, and Emmanuel Müller (2022). ‘‘Unsupervised Features Ranking via Coalitional Game Theory for Categorical Data’’. In: Big Data Analytics and Knowledge Discovery – 24th International Conference, DaWaK 2022, Vienna, Austria, August 22-24, 2022, Proceedings. Ed. by Robert Wrembel, Johann Gamper, Gabriele Kotsis, A Min Tjoa, and Ismail Khalil. Vol. 13428. Lecture Notes in Computer Science. Springer, pp. 97–111. doi: 10.1007/978-3-031-12670-3\_9. url: https://doi.org/10.1007/978-3-031-12670-3%5C_9.
• Balestra, Chiara, Bin Li, and Emmanuel Müller (2023a). ‘‘On the Consistency and Robustness of Saliency Explanations for Time Series Classification’’. In: KDD 2023, 9th International Workshop on Mining and Learning from Time Series (MILETS).
• Balestra, Chiara, Bin Li, and Emmanuel Müller (2023b). ‘‘slidSHAPs–sliding Shapley Values for correlation-based change detection in time series’’. In: 2023 IEEE 10th International Conference on Data Science and Advanced Analytics (DSAA). IEEE, pp. 1–10.
• Balestra, Chiara, Carlo Maj, Emmanuel Müller, and Andreas Mayr (2023a). ‘‘Redundancy-aware unsupervised ranking based on game theory: Ranking pathways in collections of gene sets’’. In: Plos one 18.3, e0282699.
• Balestra, Chiara, Carlo Maj, Emmanuel Müller, and Andreas Mayr (2023b). ‘‘Redundancy-aware unsupervised rankings for collections of gene sets’’. In: KDD 2023, 22nd International Workshop on Data Mining in Bioinformatics (BIOKDD).
• Balestra, Chiara, Andreas Mayr, and Emmanuel Müller (2024). ‘‘Ranking evaluation metrics from a group-theoretic perspective’’. In: arXiv preprint arXiv:2408.16009.
• Fumagalli, Fabian, Maximilian Muschalik, Patrick Kolpaczki, Eyke Hüllermeier, and Barbara Hammer (2023). ‘‘SHAP-IQ: Unified Approximation of any-order Shapley Interactions’’. In: Proceedings of Advances in Neural Information Processing Systems (NeurIPS).
• Fumagalli, Fabian, Maximilian Muschalik, Patrick Kolpaczki, Eyke Hüllermeier, and Barbara Hammer (2024). ‘‘KernelSHAP-IQ: Weighted Least Square Optimization for Shapley Interactions’’. In: Proceedings in International Conference on Machine Learning, (ICML).
• Klüttermann, Simon, Chiara Balestra, and Emmanuel Müller (2024). ‘‘On the Efficient Explanation of Outlier Detection Ensembles Through Shapley Values’’. In: Pacific-Asia Conference on Knowledge Discovery and Data Mining. Springer, pp. 43–55.
• Kolpaczki, Patrick (2024). ‘‘Comparing Shapley Value Approximation Methods for Unsupervised Feature Importance’’. In: Proceedings of DataNinja sAIOnARA 2024 Conference, pp. 13–15. doi: 10.11576/DATANINJA-1158.
• Kolpaczki, Patrick, Viktor Bengs, and Eyke Hüllermeier (2021). ‘‘Identifying Top-k Players in Cooperative Games via Shapley Bandits’’. In: Proceedings of the LWDA 2021 Workshops: FGWM, KDML, FGWI-BIA, and FGIR, pp. 133–144.
• Kolpaczki, Patrick, Viktor Bengs, Maximilian Muschalik, and Eyke Hüllermeier (2024). ‘‘Approximating the Shapley Value without Marginal Contributions’’. In: Proceedings of AAAI Conference on Artificial Intelligence (AAAI), pp. 13246–13255.
• Kolpaczki, Patrick, Georg Haselbeck, and Eyke Hüllermeier (2024). ‘‘How Much Can Stratification Improve the Approximation of Shapley Values?’’ In: Proceedings of the Second World Conference on eXplainable Artificial Intelligence (xAI), pp. 489–512.
• Kolpaczki, Patrick, Eyke Hüllermeier, and Viktor Bengs (2024). ‘‘Piecewise-Stationary Dueling Bandits’’. In: Transactions on Machine Learning Research. issn: 2835-8856.
• Kolpaczki, Patrick, Maximilian Muschalik, Fabian Fumagalli, Barbara Hammer, and Eyke Hüllermeier (2024). ‘‘SVARM-IQ: Efficient Approximation of Any-order Shapley Interactions through Stratification’’. In: Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), pp. 3520–3528.
• Li, Bin, Chiara Balestra, and Emmanuel Müller (2022). ‘‘Enabling the Visualization of Distributional Shift using Shapley Values’’. In: NeurIPS 2022 Workshop on Distribution Shifts: Connecting Methods and Applications. url: https://openreview.net/forum?id=HxnGNo2ADT.
• Muschalik, Maximilian, Hubert Baniecki, Fabian Fumagalli, Patrick Kolpaczki, Barbara Hammer, and Eyke Hüllermeier (2024). ‘‘shapiq: Shapley Interactions for Machine Learning’’. In: Proceedings Advances in Neural Information Processing Systems (NeurIPS) Datasets and Benchmarks Track.